Familiarity#
Familiarity quantifies how familiar a data point is to a specific dataset or subset, by fitting a probability distribution to the activations of the specified layer(s), and then evaluating the probability of any data sample according to the distribution.
Familiarity can be used to:
Discover the least and most representative data samples in a dataset or subset
Active learning: Use familiarity score to guide data sampling for training.
Dataset sampling: Modify the sampling strategy during training by sampling data according the the familiarity score (sample more frequently points with low score, and less frequently those that have high familiarity)
Weighted model training: Compute a weight that is inversely proportional to the familiarity score for each data sample so that such score can be used in the loss function (this can be used for training DNNs with unbalanced datasets).
Familiarity is also used in the Dataset Report to find the least and most representative data samples, in order to spot outliers, find dataset errors, and analyze data bias. Familiarity can be used on the overall dataset, or applied to subgroups of the data.
Please see the full description of the algorithm below.
General Usage#
For getting started with DNIKit code, please see the how-to pages.
Assuming a pipeline is
set up to produce responses from a model,
Familiarity can be run like so:
from dnikit.introspectors import Familiarity
producer = ... # pipeline setup here
# Run Familiarity analysis on responses from a producer
familiarity = Familiarity.introspect(producer, batch_size=128)
Preparing input to introspection usually requires two things:
introspect on intermediate layer responses (rather than the final outputs of a network). For Familiarity, the layer used will affect what kinds of features the probability distribution will represent. For example, a layer at the end of the network for a classification model will yield a Familiarity model that looks at the high level representation of the data sample: e.g. grouping similar classes together. A layer extracted from the beginning of the network might lead to a Familiarity model built around lower-level data sample information, e.g., sensor artifacts, image brightness, shape, etc. for visual data.
reduce the dimensions of outputs with a dimension reduction algorithm. This helps with the performance of the Familiarity algorithm, which tries to capture the “dense” areas of a dataset.
Familiarity is slightly different than other introspectors, in that it returns
a probability model instead of a concrete result (a Gaussian mixture model (GMM) built around the
input data, see below).
To compute Familiarity score for each data sample, or the probability of a data sample according
to the GMM, the built model in a DNIKit
pipeline will need to be applied to the data to be scored.
Full example#
A full example pipeline for the CIFAR10 dataset, using Familiarity to fit a probability distribution to the data samples with label “deer”, and then computing familiarity scores for all “deer” data. This is an example of applying Familiarity to analyzing a dataset for the least and most representative data samples, using a model not trained on the target data (MobileNet model trained on the ImageNet dataset).
from dnikit_tensorflow import TFDatasetExamples, TFModelExamples
from dnikit.introspectors import Familiarity, DimensionReduction
from dnikit.processors import Cacher, ImageResizer
from dnikit.base import pipeline
# Load CIFAR10 dataset and feed into MobileNet,
# observing responses from layer conv_pw_13
cifar10 = TFDatasetExamples.CIFAR10(attach_metadata=True)
cifar10_deers = cifar10.subset(labels=["deer"])
mobilenet = TFModelExamples.MobileNet()
producer = pipeline(
cifar10_deers,
ImageResizer(pixel_format=ImageResizer.Format.HWC, size=(224, 224)),
mobilenet(requested_responses=['conv_pw_13/convolution:0']),
Cacher()
)
# Create a processor that reduces dimensions of
# model responses down to 40, using PCA
pca = DimensionReduction.introspect(
producer,
strategies=DimensionReduction.Strategy.PCA(40)
)
# Create a new producer that outputs the reduced data:
reduced_producer = pipeline(producer, pca)
# Run Familiarity introspector
familiarity = Familiarity.introspect(reduced_producer, batch_size=64)
Note
All data samples could also be scored according to the Familiarity model instead of just the deer data, which would indicate which data samples in the overall dataset are most similar to deer according to the model and which data samples are least similar.
Exploring results#
Familiarity.introspect returns
a model instead of a concrete result. For the result to be useful, data must be scored
by feeding it through the familiarity model; e.g., in the context of the earlier example code:
scored_producer = pipeline(reduced_producer, familiarity)
This will attach metadata to each Batch of data
containing the scores for each sample, accessed via the metadata familiarity.meta_key:
for batch in scored_producer(batch_size=8):
for response_name, scores in batch.metadata[familiarity.meta_key].items():
print(response_name, scores)
The scoring is a separate step from the initial Familiarity model creation because:
Data can be scored in batches, improving efficiency for large datasets
The Familiarity model can score alternative data to what the model was fit on; for instance, to determine the most “five-like” threes in MNIST, or how close non-car CIFAR10 classes appear to “automobiles” (it’s likely trucks will come first, animal classes last).
Note
Familiarity may also be run as part of the Dataset Report and explored interactively with the Symphony UI.
Familiarity strategies#
Familiarity.introspect accepts
a strategy keyword argument that can be either the
Familiarity.Strategy.GMM strategy
or a custom strategy that follows the
FamiliarityStrategyType protocol.
See below for more information about each.
GMM (Gaussian Mixture Model)#
Fits a multivariate Gaussian Mixture Model.
GMM is a parametric density
estimation method.
The most important parameter is the number of gaussians (gaussian_count) to be learned. A
convergence_threshold can also be set that will indicate at which accuracy level the
fitting should stop (the lower the more accurate, but longer fitting time). Additionally, the
number of fitting iterations can be set through max_iterations.
The GMM strategy is suitable when it’s
known that the underlying PDF might be Gaussian (or close). However, for PDFs that are strongly
non-gaussian, a non-parametric approach might be more suitable.
It’s recommended to fit a DMM with diagonal covariance
(DIAG) when the data dimensionality is high,
to avoid overfitting and numerical instabilities. Else, use full covariance
(FULL).
Code sample for GMM familiarity
with typical parameters:
familiarity = Familiarity.introspect(
producer=response_producer,
strategy=Familiarity.Strategy.GMM(
gaussian_count=5,
covariance_type=GMMCovarianceType.DIAG,
convergence_threshold=1e-3,
max_iterations=200,
)
)
Custom Strategy#
It is also possible to define a custom Familiarity strategy that follows the
FamiliarityStrategyType protocol.
Description#
Use Case - Finding Dataset Errors#
Knowing which data points are seen as rare by a ML model and which data points have been wrongly annotated is crucial to improve model accuracy and robustness. However, inspecting datasets can become an overwhelming task as their size and complexity grows. Moreover, an ML dataset is coupled with the model that learns from it, and this dependency should not be omitted during data inspection, since it is the model that will make the final decisions.
DNIKit’s Familiarity introspector finds the most/least representative data samples in a given dataset or within a certain class. Instead of learning the distribution of the raw data, it learns the distribution of the embedding space generated by a layer of a DNN when performing inference on the dataset. Different layers capture different levels of information about the input data, and therefore, Familiarity will perform differently depending on the layer chosen.
Sometimes, for practical reasons, it is advisable to reduce the
dimensionality of the representations using a
dimension reduction
algorithm. Typical values for the reduced dimensionality are between 40 and 100,
but it depends on the use case.
The Familiarity model is fit using a dataset’s representation in embedding space, known as the model responses. The fitted model can evaluate (score) the probability for each data sample (or new data samples), where each data point \(\mathbf{x}_i\) gets a score (negative log likelihood) that tells us how dense the dataset is at embedding space position \(\mathbf{x}_i\).
Familiarity scores are useful to identify anomalies in a dataset, such as:
Wrongly labelled data, typically have a very low familiarity score.
Rare data / edge cases:
can be data that is not wanted in the dataset (eg. noisy data),
or data that should be better represented in the dataset, in that case the anomalies can guide new annotation rounds.
For finding errors within a subgroup of data, it is helpful to perform familiarity analysis for that given subgroup alone, instead of evaluating the entire dataset at once.
Use Case - Comparing Dataset Distributions#
If the train and test sets are from different distributions, then the model would be learning on data that are not representative of the real world scenario that are being tested. Similarly, a gap in distributions from two different datasets, e.g. synthetic vs. real datasets, or a new batch of data collection, can introduce problems during model training or evaluation.
Comparing the distribution of two (or more) different datasets can help to expose a hidden problem, such as with the following comparisons:
Train & test datasets: A gap indicates that the model will be / has been trained on data that are not representative of the real world scenario, as defined by the test dataset.
Original dataset with new data: A gap indicates that it’s necessary to review the datasets to learn why their distributions are different, if they’re intended to have the same distribution.
Real & synthetic datasets: A gap indicates that the synthetic data is not similar enough to the real data, as seen through the eyes of the network.
To understand the root of these problems, Familiarity is one tool available, which finds the data samples that are most unfamiliar in one dataset, when compared to the other: Dataset errors / rare samples.
To quantify the distribution, familiarity likelihood is measured as (\(\mathcal{L}_{f \rightarrow p}\)) from \(D_f=\) DATASET_FIT to \(D_p=\) DATASET_PREDICT:
If \(\mathcal{L}_{f \rightarrow p}\) is below 0.6, there is a huge gap, and one of the datasets is likely in need of being re-collected.
If \(\mathcal{L}_{f \rightarrow p}\) is between 0.6 and 0.8, then there’s a small gap, but worth further inspection.
If \(\mathcal{L}_{f \rightarrow p}\) is between 0.8 and 1.2, then there is not a significant gap between the datasets, and all looks good.
If \(\mathcal{L}_{f \rightarrow p}\) exceeds 1.2, there is a gap, and worth further inspection, with a possible re-collection of one of the datasets.
For the comparisons listed, here are some possible actions to take if there is a gap in the distributions:
Train & test datasets: In order to bridge the gap, one solution could be reshuffling of data samples across training and test sets, or collecting more data to bring the distributions together. Note: this evaluation will not help if both the training and test sets are poor representations of the target use case, but hopefully other dataset errors can be caught with some of the other dataset analysis tools in DNIKit.
Original dataset with new data: More data can be collected to bring the distributions together, and further inspect the root cause of the distribution gap using Familiarity’s Dataset errors / rare samples analysis.
Real & synthetic datasets: To bridge the gap, one solution would be to adjust the way that the synthetic data is generated, and further inspect the most unfamiliar samples using Familiarity’s Dataset errors / rare samples analysis.
To more concretely identify where there are gaps in the distribution, for datasets with class labels, compute Familiarity likelihood for each class independently.
Algorithm#
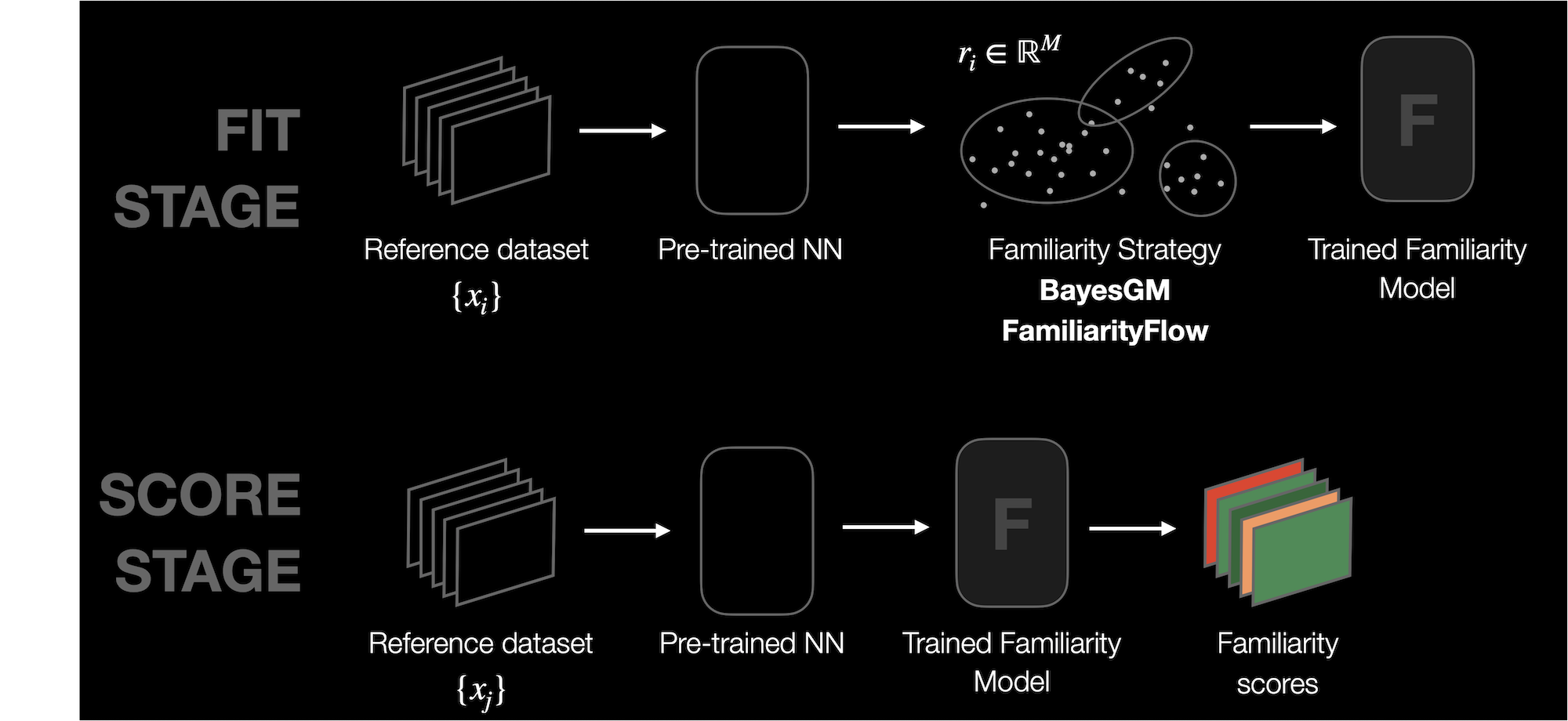
Knowing the probability density function (PDF or \(p(x)\)) underlying the observed data is of great importance for many ML domains. For example, the key idea behind algorithms like GAN or VAE is to estimate the PDF of the data as accurately as possible. However, learning a PDF in high dimensions is not trivial; furthermore the data available is typically limited. DNIKit provides different strategies to learn the probability density function of a dataset, designed to work with 1D data (i.e. responses from a DNN layer). This set of strategies is called Familiarity.
Let the response of a DNN to a data point \(x_i\) be \(r_i = \phi(x_i)\), where \(\phi\) represents the DNN. Familiarity can fit a density estimation model to a dataset \(D\) (expressed as the responses \(\{r_i\}\)). Such model learns an estimated \(\tilde{p}_{D}(r) = \tilde{p}_{D}(\phi(x))\). Note that using the responses implies learning a distribution created through the eyes of a DNN.
The trained Familiarity model can then be used to assign a score to any data point \(x_i\), either from the same training dataset or from a new one. The familiarity score tells whether a specific data point lies in a dense or non-dense area, which will be helpful for many applications.
The typical Familiarity workflow is then the following:
Run inference on a dataset \(\{x_i\}\) and obtain the corresponding responses \(\{r_i\}\) from a given DNN layer.
Fit a Familiarity model using \(\{r_i\}\) and the Familiarity strategy of choice.
Score new data (or the data used for fitting) using the model.
Being precise, the familiarity score is the negative log likelihood of the response \(r_i\) of a given data point \(x_i\):