Pruning Overview#
Pruning a model is the process of sparsifying the weight matrices of the
model’s layers, thereby reducing its storage size by packing weights more efficiently. Pruning sets a fraction of the values in the model’s weight matrices to zero.
Pruned weights can be represented more efficiently using a sparse representation rather than the typical dense representation. In a sparse representation, only non-zero values are stored, along with the indices of the non-zero values. The sparsified weights are stored using a bit mask.
For example, if the weight values are {0, 7, 0, 0, 0, 0, 0, 56.3}, its sparse representation contains a bit mask with ones in the locations where the value is non-zero: 01000001b. This is accompanied by the non-zero data, which in the following example is a size-2 vector of value {7, 56.3}.
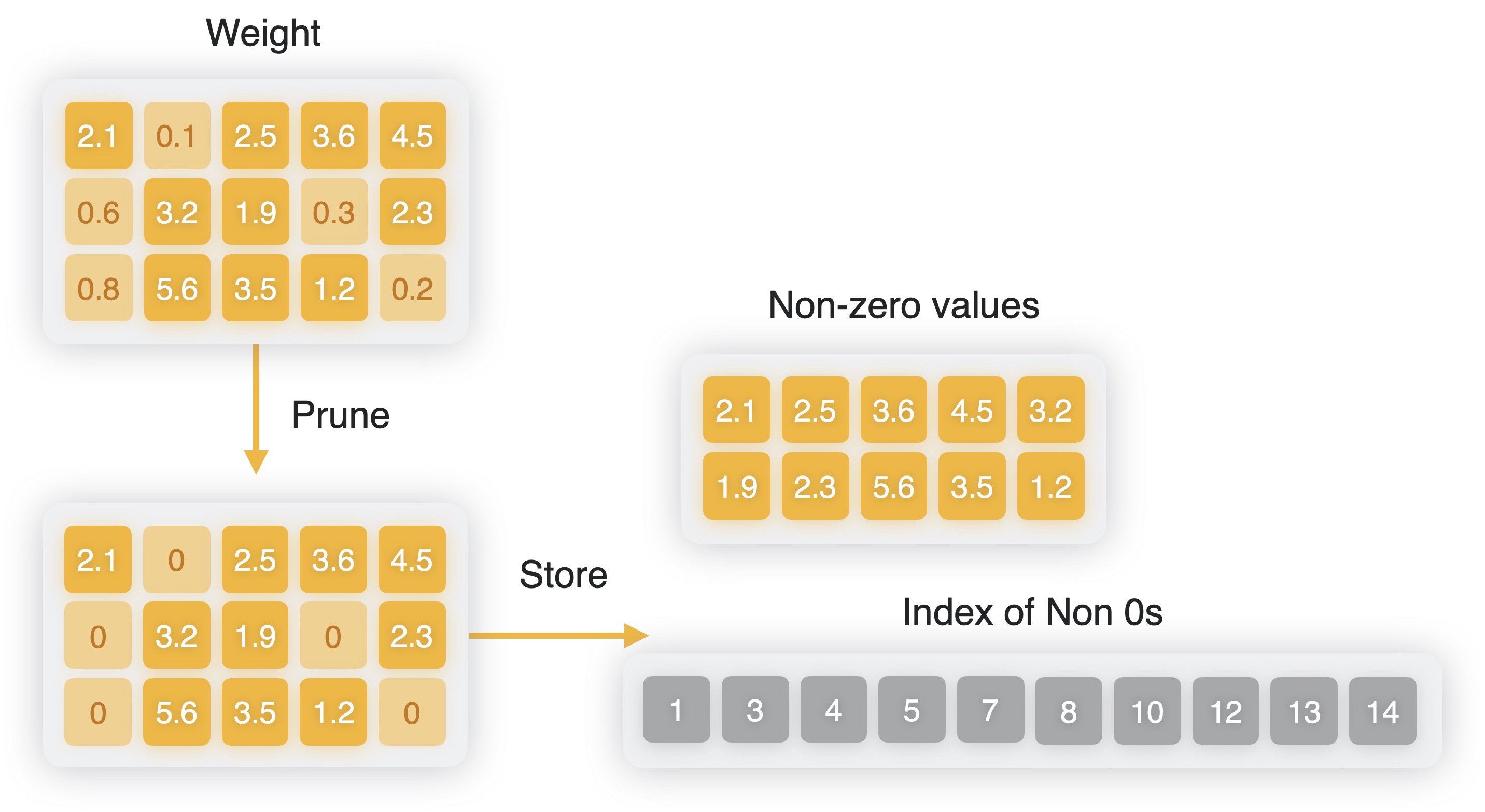
Creating a sparse representation.#
“Unstructured sparsity” is when weight values of lowest magnitude are set to zero from within the weight tensor as a whole, without adhering to any structure. On the other hand, certain constraints can be enforced while pruning, resulting in what is referred to as “structured sparsity”. A few of the common types include:
block sparsity: When weights are pruned in a grouped manner, such as in blocks of size 2, 4, and so on.n:m sparsity: When weights are divided into blocks of sizemand within each such block,nsmallest values are chosen to be zero. For example,3:4sparsity would imply a 75% sparse level in which 3 values in each block of size 4 are set to zero.
While imposing more constraints, structured sparsity techniques could be advantageous for certain hardware in terms of latency performance.
Impact on Model Size#
Compared to storing weights in a dense format with float16 precision, sparse representation saves about two bytes of storage for every zero value. Model size goes down linearly with the level of sparsity introduced.
Impact on Latency and Compute Unit Considerations#
For a model that is primarily running on the Neural Engine, sparsity typically helps in improving latency. Firstly, it reduces the amount of weight memory to be loaded at inference time, which is beneficial for networks that are weight memory bound (note that starting from iOS17/macOS14, for ops running on the Neural Engine, sparse weights are decompressed at prediction time). In addition to that, when a relatively long string of consecutive 0s are encountered, the Neural Engine may also be able to skip computations, thereby reducing the amount of computation as well. This means choosing higher levels of sparsity (e.g. 75% or higher) can lead to more latency gains than lower levels. This also means that choosing a block structured kind of sparsity with larger block sizes may be more beneficial. However, note that it’s also relatively harder to preserve accuracy with stricter constraints like larger block size and higher level of sparsity.
For a model that has a lot of linear ops and uses a specific kind of sparsity; that is, n:m such that m is a factor of 16 (such as 3:4, 7:8, 14:16, and so on), it can benefit from the CPU compute unit performance in newer hardware generations, thereby resulting in faster inference.
Note
Sparse weight compression for Core ML models is available in iOS16/macOS13/watchOS9/tvOS16 and newer deployment target formats.